MLX: Apple silicon Machine Learning - 02.Linear Regression

MLX: Linear Regression

MLX를 사용하여 간단한 Linear Regression 예제를 돌려보도록 하겠습니다.

임의의 함수를 만들어 데이터를 합성하고, 해당 데이터를 이용해 역으로 근사치를 구하는 예제입니다.

우선 관련 모듈을 import 하고 hyperparam을 세팅합니다.

import mlx.core as mx
import time

num_features = 100
num_examples = 1_000
test_examples = 100
num_iters = 10_000 # iterations of SGD
lr = 0.01 # learning rate for SGD

머신러닝에서 말하는 Batch의 정의

• 모델을 학습할 때 한 iteration당(반복 1회당) 사용되는 example의 set모임입니다.
• 여기서 iteration은 정해진 batch size를 이용하여 학습(forward - backward)를 반복하는 횟수를 말합니다.
• 한 번의 epoch를 위해 여러번의 iteration이 필요합니다.
• training error와 validation error가 동일하게 감소하다가 validation error가 증가하기 시작하는 직전 점의 epoch를 선택해야 합니다. (overfitting 방지)

Batch Size의 정의

• Batch 하나에 포함되는 example set의 갯수입니다.
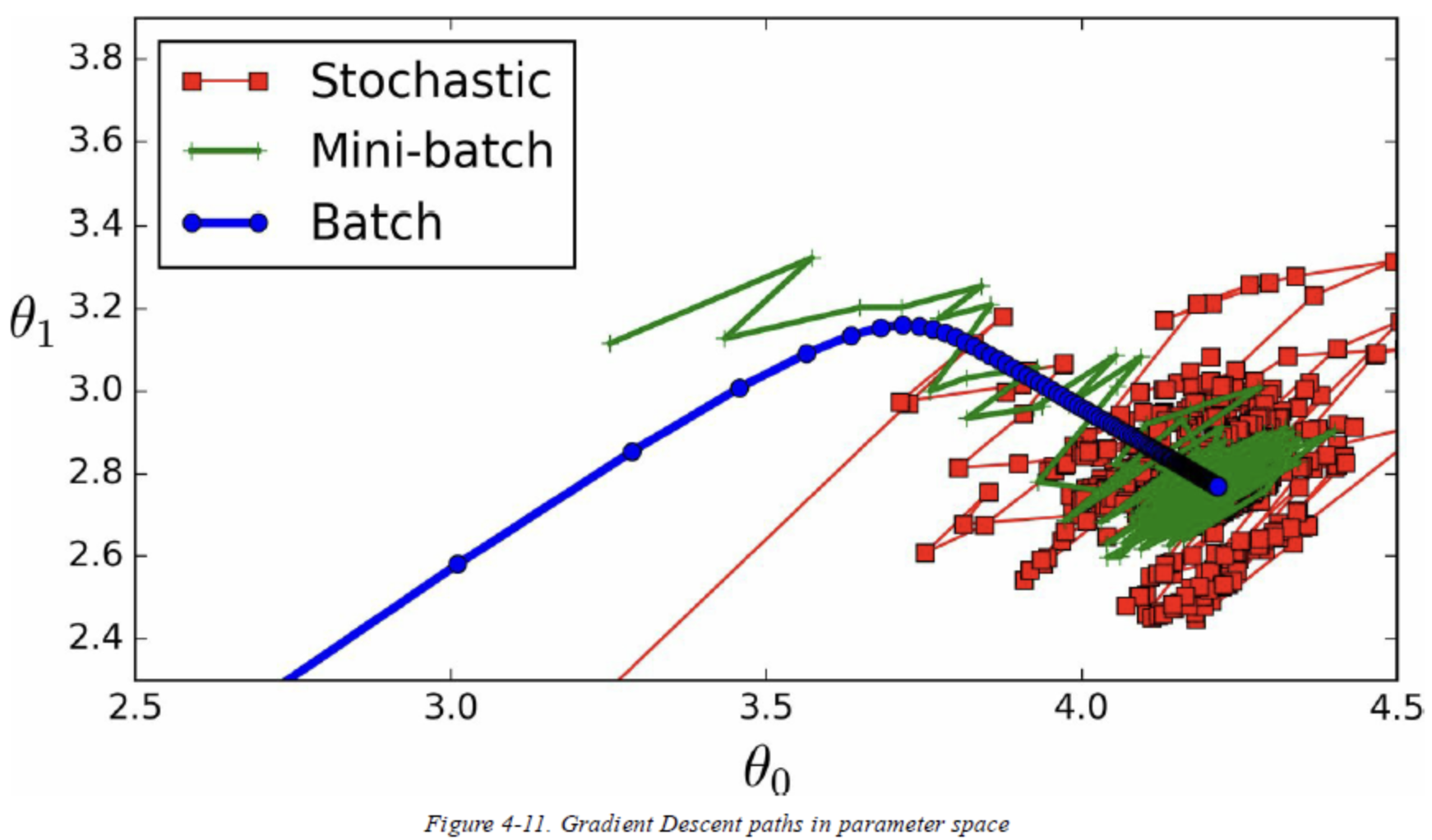
• Batch / Mini-Batch/ Stochastic 세 가지로 나눌 수 있습니다.(아래 그림 참고)

  

• SGD(Stochastic Gradient Descent)는 배치 크기가 1, Mini-Batch는 10 ~ 1,00 사이지만 보통 2의 지수승(32, 64, 128…)으로 구성됩니다.

Batch별 특징 및 장단점

Batch

• 여러개의 샘플들이 한번에 영향을 주어 합의된 방향으로 smooth하게 수렴됩니다.
• 샘플 갯수를 전부 계산해야 함으로 시간이 많이 소요됩니다.
• 모든 Training data set을 사용합니다.

(SGD)Stochastic Gradient Descent

• 데이터를 한 개씩 추출해서 처리하고 이를 모든 데이터에 반복하는 것입니다.
• 수렴 속도는 빠르지만 오차율이 큽니다. (global minimum을 찾지 못할 수 있음)
• GPU 성능을 제대로 활용하지 못하기 때문에 비효율적입니다. (하나씩 처리하기 때문)

Mini-Batch

• 전체 학습 데이터를 배치 사이즈로 등분하여 각 배치 셋을 순차적으로 수행합니다.
• 배치보다 빠르고 SGD보다 낮은 오차율을 가지고 있습니다.

임의의 선형 함수를 만들고, 임의의 input 데이터를 만들어줍니다.

mx.random.normal을 이용하여 랜덤하게 만들어줍니다.

label 값의 경우 만들어진 input데이터를 함수에 통과시키고, 작은 noise를 부여하여 만들어줍니다.

# 임의의 선형 함수 True parameters
w_start = mx.random.normal((num_features,))

# Input examples(design matrix)
X = mx.random.normal((num_examples, num_features))

# Noisy labels
eps = 1e-2 * mx.random.normal((num_examples,))
mx.random.normal((num_examples,))
y = X @ w_start + eps

• @는 NumPy나 MXNet과 같은 배열 계산 라이브러리에서 행렬 곱셈(또는 행렬-벡터 곱셈)을 나타내는 연산자입니다.
• X @ w_start는 행렬 X와 벡터 w_start사이의 행렬 곱셉을 의미합니다.

별도의 테스트 셋도 만들어줍니다.

# Test set generation
X_test = mx.random.normal((test_examples, num_features))
y_test = X_test @ w_start

그리고 Loss function과 Gradient function(mx.grad 사용)을 만들어줍니다.

# MSE Loss function
def loss_fn(w):
    return 0.5 * mx.mean(mx.square(X @ w - y))

# Gradient function
grad_fn = mx.grad(loss_fn)

이제 Linear regression을 위한 parameter를 초기화하고 SGD(Stochastic Gradient Descent) 방법을 이용해 학습합니다.

# Initialize random parameter
w = 1e-2 * mx.random.normal((num_features,))

# Test Error(MSE)
pred_test = X_test @ w
test_error = mx.mean(mx.square(y_test - pred_test))

print(f"Initial Test Error(MSE): {test_error.item():.6f}")

Initial Test Error(MSE): 114.406784

# Training by SGD
start = time.time()
for its in range(1,num_iters+1):
    grad = grad_fn(w)
    w = w - lr * grad
mx.eval(w)
end = time.time()

print(f"Training elapsed time: {end-start} seconds")
print(f"Throughput: {num_iters/(end-start):.3f} iter/s")

Training elapsed time: 0.8959159851074219 seconds
Throughput: 11161.761 iter/s

# Test Error(MSE)
pred_test = X_test @ w
test_error = mx.mean(mx.square(y_test - pred_test))

print(f"Final Test Error(MSE): {test_error.item():.6f}")

Final Test Error(MSE): 0.000011

Test Set애서 MSE값이 크게 감소한 것을 확인할 수 있습니다.(Test Set MSE: 0.00001)

추가적으로 수행시간은 약 0.8초 걸린 것을 확인할 수 있습니다.(M3 Macbook pro 기준)

CPU 연산과의 수행시간 비교

만약 MLX(GPU)대신에 numpy array(CPU)를 사용했을 때 발생되는 속도 차이를 살펴보겠습니다.

import numpy as np

# True parameters
w_star = np.random.normal(size=(num_features,1))

# Input examples(design matrix)
X = np.random.normal(size=(num_examples, num_features))

# Noisy labels
eps = 1e-2 * np.random.normal(size=(num_examples,1))
y = np.matmul(X, w_star) + eps

# Test Set Generation
X_test = np.random.normal(size=(test_examples, num_features))
y_test = np.matmul(X_test, w_star)

def loss_fn(w):
    return 0.5 * np.mean(np.square(np.matmul(X, w) - y))

def grad_fn(w):
    return np.matmul(X.T, np.matmul(X, w) - y) * (1/num_examples)

w = 1e-2 * np.random.normal(size = (num_features,1))

pred_test = np.matmul(X_test, w)
test_error = np.mean(np.square(y_test - pred_test))

print(f"Initial Test Error(MSE): {test_error.item():.6f}")

Initial Test Error(MSE): 93.005015

start = time.time()
for its in range(1,num_iters+1):
    grad = grad_fn(w)
    w = w - lr * grad

end = time.time()

print(f"Training elapsed time: {end-start} seconds")
print(f"Throughput: {num_iters/(end-start):.3f} iter/s")

Training elapsed time: 0.8565518856048584 seconds
Throughput: 11674.716 iter/s

pred_test = np.matmul(X_test, w)
test_error = np.mean(np.square(y_test - pred_test))

print(f"Final Test Error(MSE): {test_error.item():.6f}")

Final Test Error(MSE): 0.000010

간단한 linear regression에서는 큰 차이가 없는 것을 확인할 수 있었습니다.

multi-layer perceptron처럼 행렬 연산이 무거워지는 경우 차이가 발생하는지 다음 포스팅에서 확인해 보도록 하겠습니다.

References

• MLX 홈페이지(MLX Linear Regression 설명)

• Tstory(Batch 설명)

• SKT Enterprise(MLX Linear Regression 설명)